
Progressão geométrica é toda sequência numérica em que cada termo, a partir do segundo, é igual ao produto do termo anterior por uma constante q.
Propriedades da PG
Numa PG positiva qualquer termo é a média geométrica entre o termo anterior e o seguinte. Assim, na PG (1, 2, 4, 8, 16, 32), temos:
4 é a média geométrica entre 2 e 8, porque 4 =
2⋅8−−−−
√
;
8 é a média geométrica entre 4 e 16, porque 8 =
4⋅16−−−−
√
.
É importante saber fazer a representação de uma PG genérica, por exemplo:
(x,
x⋅q
,
x⋅
q
2
,
x⋅
q
3
...), com razão q.
CLASSIFICAÇÃO
As progressões geométricas, da mesma forma que as progressões aritméticas, classificam-se em finitas, infinitas, decrescentes, crescentes e estacionárias. Além disso, as progressões geométricas de razão negativa são chamadas de alternadas, porque seus termos são alternadamente positivos e negativos.
Uma PG é crescente quando cada termo, a partir do segundo, é maior que o termo que o antecede. Para que isso aconteça é necessário e suficiente que a
1
> 0 e q > 1, ou a1
< 0 e 0 < q < 1. Por exemplo:
(4, 8, 16, 32...) é uma PG crescente de razão q = 2;
(-4, -2, -1,
−12
...) é uma PG decrescente de razão q = 12
.
Uma P.G. é constante quando todos os seus termos são iguais. Para isso aconteça é necessário e suficiente que sua razão seja 1 ou que todos os seus termos sejam nulos. Observe:
(8, 8, 8, 8...) é uma PG constante de razão q = 1.
(0, 0, 0, 0...) é uma PG constante de razão indeterminada.
Uma PG é oscilante quando todos os seus termos são diferentes de zero e dois termos consecutivos quaisquer têm sinais opostos. Para que isso aconteça, é necessário e suficiente que
a1
≠0
e q < 0. Veja:
(3, -6, 12, -24, 48, -96...) é uma PG oscilante de razão q = -2.
(-1,
12
, −14
, 18
, −116
...) é uma PG oscilante de razão q = −12
.
Uma PG é quase nula quando o primeiro termo é diferente de zero e todos os demais são iguais a zero. Para que isso aconteça, é necessário e suficiente que a
1
≠0
e q = 0. Por exemplo:
(8, 0, 0, 0, 0...) é uma P.G. quase nula.
EXEMPLOS
A sequência seguinte é uma progressão geométrica, observe: (2, 6, 18, 54...). Determine o 8º termo dessa progressão.
Razão da progressão: 6 : 2 = 3
an = a1 * q n–1
a8 = 2 * 3 8–1
a8 = 2 * 3 7
a8 = 2 * 2187
a8 = 4374
(Vunesp – SP – Adaptado)
Várias tábuas iguais estão em uma madeireira. Elas deverão ser empilhadas respeitando a seguinte ordem: uma tábua na primeira vez e, em cada uma das vezes seguintes, tantas quantas já estejam na pilha. Por exemplo:
Determine a quantidade de tábuas empilhadas na 12ª pilha.
As tábuas são empilhadas de acordo com uma progressão geométrica de razão 2. Então:
an = a1 * q n–1
a12 = 1 * 2 12–1
a12 = 1 * 2 11
a12 = 1 * 2048
a12 = 2048
Na 12ª pilha teremos 2048 tábuas.
Determine o décimo termo de uma progressão geométrica cujo primeiro termo é 2 e a razão é 3.
A fórmula usada para determinar um termo qualquer de uma PG é:
an = a1·qn – 1
Substituindo os valores nessa fórmula, teremos:
an = a1·qn – 1
a10 = 2·310 – 1
a10 = 2·39
a10 = 2·19683
a10 = 39366
Qual é o décimo quinto termo da PG (1, 2, 4, 8, …)?
Para encontrar o 15º termo da PG, basta usar a fórmula do termo geral:
an = a1·qn – 1
Note que a razão da PG é 2, pois esse é o resultado da divisão de qualquer termo por seu antecessor. Por exemplo, 2 : 1 = 2. Substituindo os valores na fórmula, teremos:
a15 = 1·215 – 1
a15 = 215 – 1
a15 = 214
a15 = 16384
Determine o décimo termo da PG (−14, 12, -1...)
Resposta
a10 = ?
a1 = −14
q = -2
a10 = a1⋅qn−1
a10 = −14⋅29
a10 = 4−1⋅29
a10 = 22(−1)⋅29
a10 = 2−2⋅29
a10 = 27 = 128
I

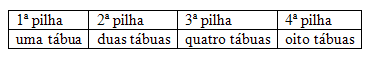


Shouw
ResponderExcluir