Ondas
Para a Física, a onda é uma perturbação que se propaga no espaço ou em qualquer outro meio. Elas são classificadas em relação à natureza, direção e energia de propagação.
As ondas são perturbações que se propagam no espaço ou em meios materiais transportando energia. De acordo com a sua natureza, as ondas podem ser classificadas em dois tipos:
Ondas mecânicas: são as ondas que se propagam em meios materiais. Por exemplo: as ondas marítimas, ondas sonoras, ondas sísmicas etc. A descrição do comportamento desse tipo de onda é feita pelas Leis de Newton.
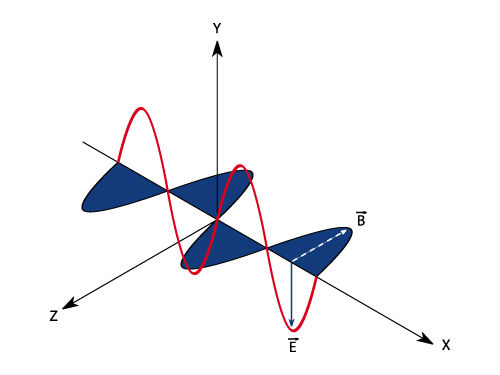
Ondas eletromagnéticas: são resultado da combinação de campo elétrico com campo magnético. A sua principal característica é que não precisam de um meio material para propagar-se. São exemplos desse tipo de onda a luz, raio X, micro-ondas, ondas de transmissão de sinais, entre outras. Elas são descritas pelas equações de Maxwell.
Outra classificação das ondas é feita considerando-se a direção de vibração. De acordo com essa característica, uma onda pode ser definida como:
→ Transversal: quando as partículas do meio de propagação vibram perpendicularmente à direção de propagação da onda. Um exemplo desse tipo de onda é a luz.
→ Longitudinais: quando as partículas do meio de propagação vibram na mesma direção em que a onda se propaga, como é o caso das ondas sonoras.
Por fim, quanto à direção de propagação, as ondas podem ser classificadas em:
→ unidimensionais: quando se propagam em apenas uma direção, como a onda em uma corda;
→ bidimensionais: se a propagação ocorre em duas direções, que é o caso da onda gerada por uma perturbação na água;
Propriedades das ondas
Para estudar uma onda, precisamos conhecer algumas de suas propriedades, tais como: a velocidade de propagação, a amplitude, o período e a frequência. Para uma melhor compreensão dessas propriedades, veja a seguir a representação gráfica de uma onda:
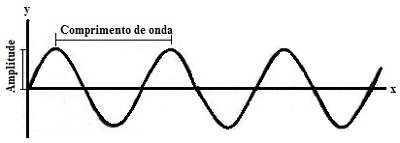
Representação gráfica de uma onda
O comprimento de onda, que pode ser representado pela letra λ, é a distância entre valores repetidos em uma forma de onda. É calculado com a equação:
Sendo:
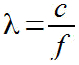
λ – o comprimento de onda;
c – velocidade da luz no vácuo (possui valor igual a 3.108m/s);
f – frequência da luz.
A partir de λ, podemos calcular a velocidade de uma onda com a seguinte fórmula:
Sendo:
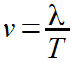
v – velocidade da onda;
λ – comprimento da onda;
T – período.
O período é definido como o espaço de tempo necessário para uma onda caminhar um comprimento de onda.
A frequência é o inverso do período:
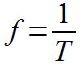
a velocidade de propagação da onda pode ser dada por:
Exemplos
QUESTÃO 1
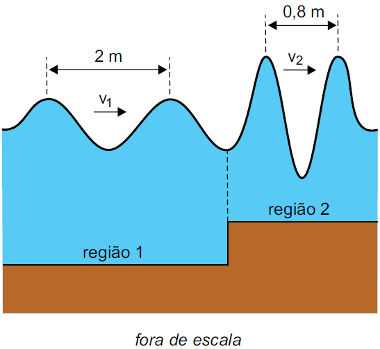
(FAMEMA-SP) Com o objetivo de simular as ondas no mar, foram geradas, em uma cuba de ondas de um laboratório, as ondas bidimensionais representadas na figura, que se propagam de uma região mais funda (região 1) para uma região mais rasa (região 2).

Sabendo que, quando as ondas passam de uma região para a outra, sua frequência de oscilação não se altera e considerando as medidas indicadas na figura, é correto afirmar que a razão entre as velocidades de propagação das ondas nas regiões 1 e 2 é igual a:
a) 1,6.
b) 0,4.
c) 2,8.
d) 2,5.
e) 1,2.
QUESTÃO 2
(IFGO) As ondas são formas de transferência de energia de uma região para outra. Existem ondas mecânicas – que precisam de meios materiais para se propagarem – e ondas eletromagnéticas – que podem se propagar tanto no vácuo como em alguns meios materiais. Sobre ondas, podemos afirmar corretamente que
a) a energia transferida por uma onda eletromagnética é diretamente proporcional à frequência dessa onda.
b) o som é uma espécie de onda eletromagnética e, por isso, pode ser transmitido de uma antena à outra, como ocorre nas transmissões de TV e rádio.
c) a luz visível é uma onda mecânica que somente se propaga de forma transversal.
d) existem ondas eletromagnéticas que são visíveis aos olhos humanos, como o ultravioleta, o infravermelho e as micro-ondas.
e) o infrassom é uma onda eletromagnética com frequência abaixo da audível.
QUESTÃO 3
A respeito das características das ondas, marque a alternativa errada.
a) Ondas sonoras e ondas sísmicas são exemplos de ondas mecânicas.
b) A descrição do comportamento das ondas mecânicas é feita pelas leis de Newton.
c) As ondas eletromagnéticas resultam da combinação de um campo elétrico com um campo magnético.
d) A descrição das ondas eletromagnéticas é feita por meio das equações de Maxwell.
e) Quanto à direção de propagação, as ondas geradas em um lago pela queda de uma pedra na água são classificadas como tridimensionais.
QUESTÃO 4
O som mais grave que o ouvido humano é capaz de ouvir possui comprimento de onda igual a 17 m. Sendo assim, determine a mínima frequência capaz de ser percebida pelo ouvido humano.
Dados: Velocidade do som no ar = 340 m/s
a) 10 Hz
b) 15 Hz
c) 17 Hz
d) 20 Hz
e) 34 Hz
RESPOSTAS
Questão 1
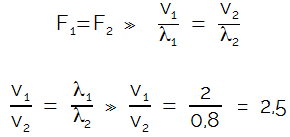
LETRA “D”
Os valores 2 m e 0,8 m representam os comprimentos das ondas nas regiões 1 e 2, respectivamente.
A frequência das ondas deve ser a mesma nas duas regiões, pois, na mudança de lugar de propagação, a frequência de uma onda não é alterada. Sendo assim, temos:
F1 = F2
Sabendo que a velocidade de uma onda é dada pelo produto do comprimento de onda e a velocidade, podemos entender que a frequência é a razão da velocidade pelo comprimento de onda:
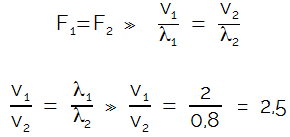
Questão 2
LETRA “A”
a) CORRETA
b) ERRADO: O som é uma onda mecânica.
c) ERRADO: A luz visível é uma onda eletromagnética.
d) ERRADO: O ultravioleta e infravermelho não são ondas que compõem o espectro visível.
e) ERRADO: O infrassom é uma onda mecânica com frequência abaixo do audível.
Questão 3
LETRA “E”
As ondas geradas em um lago pela queda de uma pedra na água são classificadas como bidimensionais, pois existem apenas sobre a superfície da água.
Questão 4
LETRA “D”
A partir da equação da velocidade de uma onda, podemos escrever que:
v = λ . f
f = v ÷ λ
f = 340 ÷ 17
f = 20 Hz


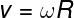
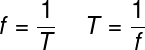

.gif)


.jpg)