Exercícios Sobre Progressão Aritmética

Questão 1

Em relação à progressão aritmética (10, 17, 24, …), determine:

a) o termo geral dessa PA;

b) o seu 15° termo;

c) a soma a₁₀ + a ₂₀.

Questão 2

Determine:

a) a soma dos 10 primeiros termos da PA (2, 5, …);

b) a soma dos 15 primeiros termos da PA (– 1, – 7, …);

c) a soma dos 20 primeiros termos da PA (0,5; 0,75, …).

Questão 3

(IBMEC – SP) Um número triangular é um inteiro da forma , sendo n um inteiro positivo. Considere a tabela:

Posição	1	2	3	...	X	...
Triangular	1	3	6	...	3486	...

A soma dos algarismos de X é:

a) 10

b) 11

c) 12

d) 13

e) 14

Questão 4

(Puc – RS) Tales, um aluno do Curso de Matemática, depois de terminar o semestre com êxito, resolveu viajar para a Europa. O portão de Brandeburgo, em Berlim, possui cinco entradas, cada uma com 11 metros de comprimento. Tales passou uma vez pela primeira porta, duas vezes pela segunda e assim sucessivamente, até passar cinco vezes pela quinta. Então ele percorreu ____ metros.

a) 55

b) 66

c) 165

d) 275

e) 330

Respostas

Resposta Questão 1

a) Para encontrar o termo geral da progressão aritmética, devemos, primeiramente, determinar a razão r:

r = a₂ – a₁

r = 17 – 10

r = 7

A razão é 7, e o primeiro termo da progressão (a₁) é 10. Através da fórmula do termo geral da PA, temos:

a_n = a₁ + (n – 1). r

a_n = 10 + (n – 1). 7

Portanto, o termo geral da progressão é dado por a_n = 10 + (n – 1). 7.

b) Como já encontramos a fórmula do termo geral, vamos utilizá-la para encontrar o 15° termo. Tendo em vista que n = 15, temos então:

a_n = 10 + (n – 1). 7

a₁₅ = 10 + (15 – 1). 7

a₁₅ = 10 + 14 . 7

a₁₅ = 10 + 98

a₁₅ = 108

O 15° termo da progressão é 108.

c) Vamos utilizar a fórmula do termo geral para identificar os elementos a₁₀ e a₂₀ da PA:

a_n = 10 + (n – 1). 7

a₁₀ = 10 + (10 – 1). 7

a₁₀ = 10 + 9 . 7

a₁₀ = 10 + 63

a₁₀ = 73

a_n = 10 + (n – 1). 7

a₂₀ = 10 + (20 – 1). 7

a₂₀ = 10 + 19 . 7

a₂₀ = 10 + 133

a₂₀ = 143

A soma a₁₀ + a ₂₀ é dada por:

a₁₀ + a ₂₀ = 73 + 143 = 216

Resposta Questão 2

a) Para encontrar a soma dos 10 primeiros termos da PA (2, 5, …), precisamos identificar a razão e o termo a₁₀. A razão pode ser encontrada pela subtração entre o primeiro termo e o segundo, ou seja, r = 5 – 2 = 3. Vamos utilizar a fórmula do termo geral para encontrar o 10° termo dessa sequência:

a_n = a₁ + (n – 1). r

a₁₀ = 2 + (10 – 1). 3

a₁₀ = 2 + 9 . 3

a₁₀ = 2 + 27

a₁₀ = 29

Agora utilizaremos a fórmula da soma dos termos de uma PA finita. Sabendo que o primeiro termo da progressão é 2 e que n = 10, temos:

S_n = (a₁ + a_n) . n

       2

S₁₀ = (2 + 29) . 10

         2

S₁₀ = 31 . 10

         2

S₁₀ = 155

A soma dos 10 primeiros termos da PA (2, 5, …) é 155.

b) Inicialmente, vamos identificar a razão e o termo a₁₅. A razão é dada por:

r = – 7 – (– 1)

r = – 7 + 1

r = – 6

Através da fórmula do termo geral, vamos encontrar o 15° termo da PA:

a_n = a₁ + (n – 1). r

a₁₅ = – 1 + (15 – 1). (– 6)

a₁₅ = – 1 + 14 . (– 6)

a₁₅ = – 1 – 84

a₁₅ = – 85

Agora utilizaremos a fórmula da soma dos termos de uma PA finita. Como n = 15, temos:

S_n = (a₁ + a_n) . n

       2

S₁₅ = [(– 1) + (– 85)] . 15

         2

S₁₅ = (– 86) . 15

         2

S₁₅ = – 645

Portanto, a soma dos 15 primeiros termos da PA (– 1, – 7, …) é – 645.

c) Precisamos identificar a razão da PA:

r = 0,75 – 0,5

r = 0,25

Através do termo geral, encontramos o 20° termo dessa sequência:

a_n = a₁ + (n – 1). r

a₂₀ = 0,5 + (20 – 1). 0,25

a₂₀ = 0,5 + 19 . 0,25

a₂₀ = 0,5 + 4,75

a₂₀ = 5,25

Pela fórmula da soma dos termos de uma PA finita, temos:

S_n = (a₁ + a_n) . n

       2

S₂₀ = (0,5 + 5,25) . 20

        2

S₂₀ = 5,75 . 20

        2

S₂₀ = 57,5

A soma dos 20 primeiros termos da PA (0,5; 0,75; …) é 57,5.

Resposta Questão 3

A progressão aritmética em questão é formada pelos números triangulares da tabela em que a₁ = 1, a₂ = 3, a₃ = 6 e a_x = 3486. Resta-nos identificar o valor de X para que possamos encontrar a soma de seus algarismos. Observe que a fórmula que fornece os números triangulares assemelha-se à fórmula da soma dos termos de uma PA. Se substituirmos a variável n por X, teremos o número triangular 3486:

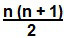 → X . (X + 1) = 3486

           2

X . (X + 1) = 6972

X² + X – 6972 = 0

Utilizaremos a fórmula de Bhaskara para encontrar o valor de X:

Δ = 1² – 4.1.(– 6972)

Δ = 1 + 27888

Δ = 27889

x = – 1 ± √27889

        2.1

x = – 1 ± 167

      2

x' = 166 = 83

2

x'' = – 168 = – 84

2

Nesse caso, a equação tem duas raízes reais, – 84 e 83, mas como X não pode ser negativo, pois as posições da tabela não estão decrescendo, podemos afirmar que X = 83. Sendo assim, a soma dos algarismos de X é dada por 8 + 3 = 11. Portanto, a alternativa correta é a letra b.

Resposta Questão 4

Quando Tales passou pela primeira entrada, ele percorreu 11 metros; ao passar pela segunda entrada duas vezes, ele percorreu (11 . 2 ) 22 metros e dessa maneira Tales prosseguiu até que passou cinco vezes pela quinta entrada (11 . 5), percorrendo 55 metros. Podemos formar uma PA com essas informações, sendo que a₁ = 11 e a₅ = 55. Através da fórmula da soma dos termos de uma PA finita, podemos identificar quantos metros Tales andou:

S_n = (a₁ + a_n) . n

       2

S₅ = (11 + 55) . 5

       2

S₅ = 66 . 5

       2

S₅ = 165

Portanto, Tales andou um total de 165 metros e a alternativa correta é a letra c.